In a previous post we have seen that twisted light with orbital angular momentum $\ell=+1$ and circular polarization $\sigma =-1$ close to the beam axis has a strong electric field component in the direction of propagation ($z$) that doesn't vanish at $r=0$. We noted that this longitudinal electric field can excite light-hole quantum dot (QD) excitons with zero band+spin angular momentum. This has interesting applications to spintronics and quantum computing. We explain in what follows how the zero angular momentum exciton state is ideal to control the spin state of an extra electron siting on a QD.
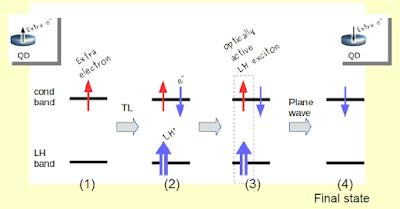
Imagine that we have a QD charged with a single extra electron. Initially it could be in any possible spin state, for example up (quantized in z) as depicted in Fig. 1 (upper left corner). We wish to use light beams at normal incidence [Footnote1] to flip the spin and have a final state as the one in Fig. 1 (upper right corner).
 | |
|
Figure 1 suggests that only a pure spin up (or down) state can be flipped. But a computer simulation using density matrix shows that any arbitrary superposition spin-state can be inverted using a sequence of three pulses that are independent of the initial state of the QD. We show this in Fig. 2.
 |
| Figure 2: Computer simulations using density matrix. Spin flip of a superposition state is achieved in less than a picosecond. P's represent the normal-incidence pulses. |
A possible semiconductor-based quantum computer would employ QD or impurity spins as qubits. To realize any complex logical operation one would require full control on the single spin + on the interaction between two different spins. To fully control the single spin one needs to be able to flip it along any axis: we just showed how to do it along z using twisted light, but there are different ways to flip it in the x-y plane, for example using exciton-polaritons in microcavities [2]. On the other hand, the control of the interaction between two spins can also be accomplished using exciton-polaritons [3]. Since twisted light can be confined in semiconductor microcavities, it seems that we now know how to implement all possible logical operations in this type of solid-state quantum computer.
References
[Footnote1] We envisage a planar system containing many dots, where each dot can be addressed by the light beam. Then, from a technological point of view we want to use only light at normal incidence.
[1] Quinteiro, G. F., and T. Kuhn. "Light-hole transitions in quantum dots: Realizing full control by highly focused optical-vortex beams." Physical Review B 90, no. 11 (2014): 115401.
[2] Quinteiro, G. F., P. Dmitruk, and A. A. Aligia. "Efficient spin control in high-quality-factor planar microcavities." Physical Review B 86, no. 3 (2012): 035329.
[3] Quinteiro, G. F., Joaquín Fernández-Rossier, and C. Piermarocchi. "Long-range spin-qubit interaction mediated by microcavity polaritons." Physical review letters 97, no. 9 (2006): 097401.






0 comments:
Post a Comment